On the subgroup lattice of a group
A couple of months ago, I went to a very enjoyable conference in Florence. During the course of this conference, I found myself stood in a coffee queue next to Peter Pal Palfy, whom I had heard of but never had the privilege of meeting. I want to recount a very interesting bit of maths that he told me about while we were in that queue – although it concerns a very natural group theory question, I had never heard of it before.
Anyone who has done a little bit of group theory is familiar with the subgroup lattice of a group. This question concerns what can happen between a second-maximal subgroup of a group G, and the group G itself.
A second-maximal subgroup, H, of G is a group that is maximal in the lattice of subgroups of G, once we have removed G itself, along with all maximal subgroups of G. By definition, the only proper subgroups that contain such a group H are maximal subgroups of G. So we have this set-up:
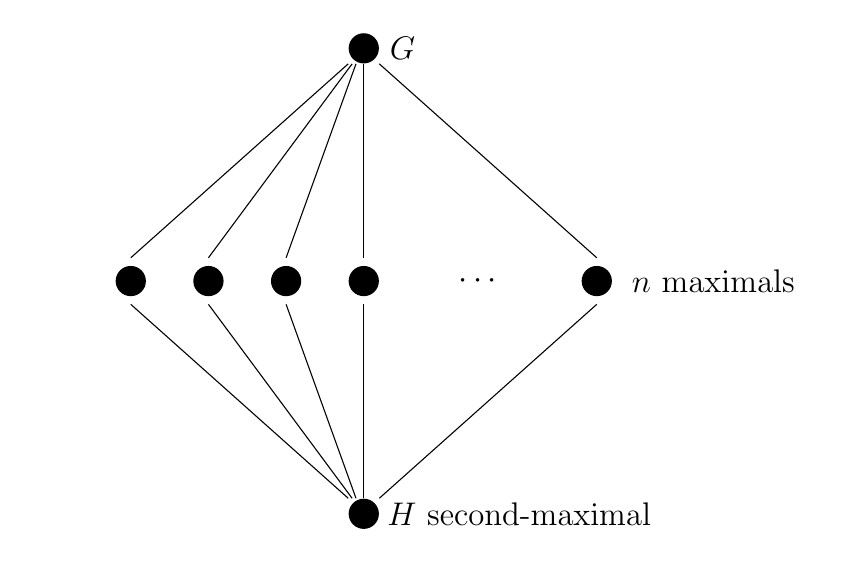
So, observe, that our second-maximal subgroup H lies inside precisely n maximal subgroups of G. Now, here’s the question: what are the possibilities for the number n in the diagram?
For instance, is it possible to find a group G which has a second-maximal subgroup H that lies in precisely 8 maximal subgroups of G. If the answer is “yes” to this question, then let’s say that 8 is an sml-number.
A preliminary observation: If G is elementary abelian of order p^2 for some prime p, then the trivial subgroup is second-maximal, and basic linear algebra says that it lies in precisely 1+p maximal subgroups of G. Thus, p+1 is an sml-number, for every prime p.
With a bit of ingenuity, one can generalize this example to conclude that q+1 is an sml-number, for every prime power q. What is more one can construct these examples so that the groups in question are solvable. Now, here’s a neat partial converse, due to Palfy and Pudlak: If H is a second-maximal subgroup of a solvable group G, then H is contained in q+1 maximal subgroups for some prime power q.
For solvable groups, then, we have a complete answer. What about non-solvable groups? Here, the situation is still unclear. A 1983 paper of Walter Feit established that both 7 and 11 are sml-number – remarkably, he does this by exhibiting two different second maximal subgroups H of the alternating group A_31, one of which lies in exactly 7 maximals (here H is the normalizer of a Sylow 31-subgroup in PSL(5,2)), the other in 11 (here H is the normalizer of a Sylow 31-subgroup in PSL(3,5)).
Subsequent work by Lucchini has shown that all numbers of the form q+2 are sml-numbers for q a prime power. He has exhibited other infinite families of sml-numbers, although as far as I know Feit’s examples remain sporadic.
To my knowledge, a complete answer still remains to be proven. I find it quite remarkable that such a basic question should throw up such bizarre and sporadic behaviour, and thereby resist a complete solution…